Университет Лекции По Математике

• Гдз По Математике 8 Класс
• Гдз По Математике 5 Класс

Лекции читает Павел Константинович Катышев (Старший научный сотрудник ЦЭМИ РАН, профессор кафедры математических. Информация для желающих обучаться. Математика ДВИ (доп. Набор) Постановка на воинский.

Лекции по алгебре, Фаддеев Д.К., 2007. Учебное пособие представляет собой изложение курса лекций по алгебре, читавшегося автором в Санкт-Петербургском государственном университете на протяжении ряда лет.

Этот курс рассчитан на 3 семестра. Большим достоинством книги является то, что абстрактные понятия вводятся в ней как результаты обобщения конкретного математического материала. Для студентов университетов и пединститутов. Некоторые общие понятия алгебры.

В теории сравнений мы встретились с новым явлением, имеющим большую принципиальную важность. Мы обнаружили математические объекты, именно, классы по модулю, не являющиеся числами, но над которыми мы имеем возможность совершать алгебраические действия. Свойства этих действий напоминают свойства действий над числами. Подобного рода системы объектов возникают в математике в разнообразных ситуациях, и это делает естественной и необходимой формализацию возникающих на этом пути более общих понятий. Полугруппой называется множество, в котором определено действие, сопоставляющее каждой упорядоченной паре элементов третий — результат действия. Действие предполагается ассоциативным. Полугруппами являются: множество целых неотрицательных чисел относительно действия сложения, то же множество относительно действия умножения (это совсем другая полугруппа), множество классов по модулю относительно умножения.

Во всех этих примерах действие коммутативно. Оглавление Предисловие Глава I ЦЕЛЫЕ ЧИСЛА §1. Теория делимости целых чисел §2. Теория сравнений §3.

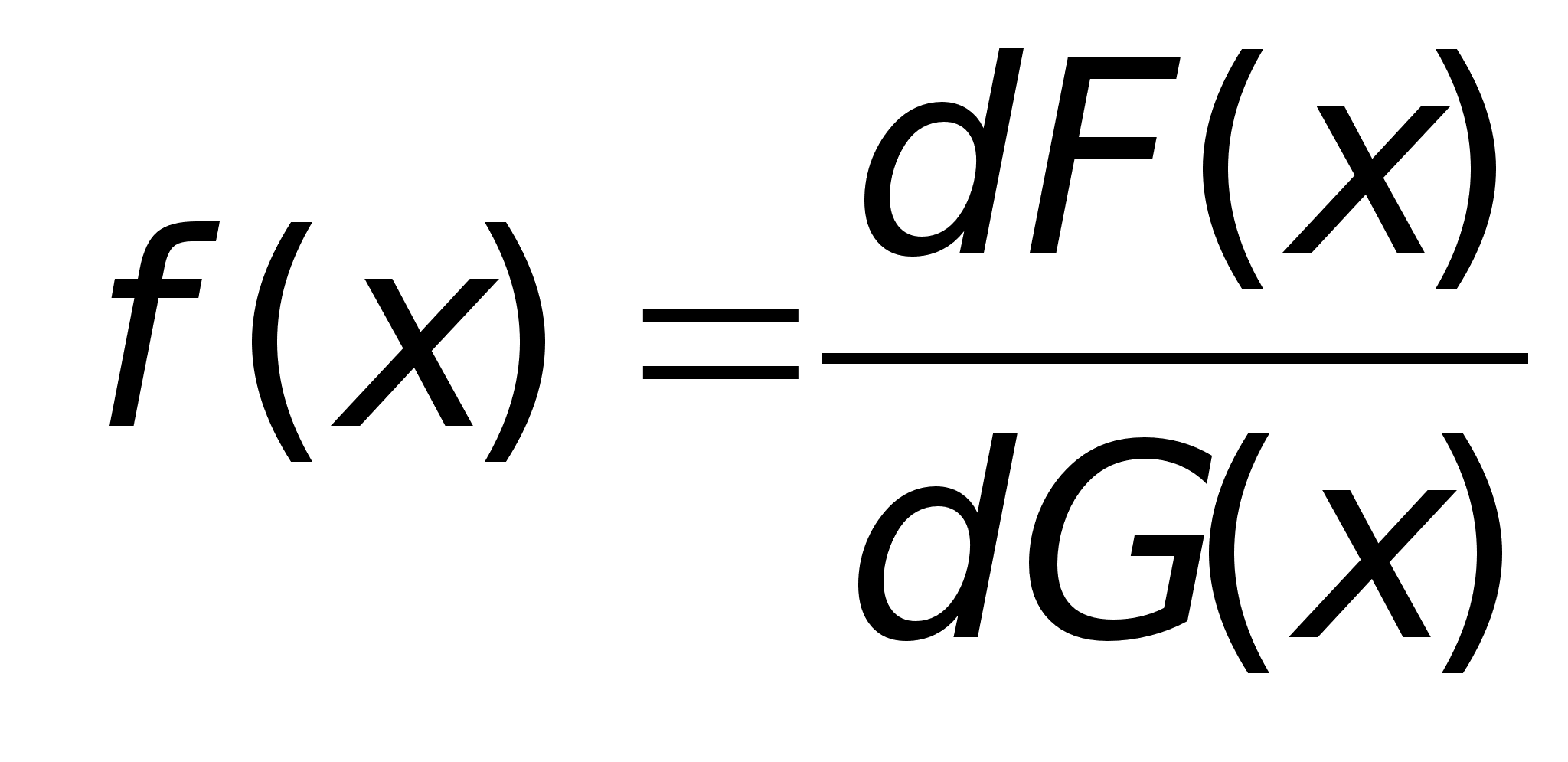
Некоторые общие понятия алгебры Глава II КОМПЛЕКСНЫЕ ЧИСЛА §1. Обоснование комплексных чисел §2. Тригонометрическая форма комплексного числа §3. Извлечение корня из комплексного числа §4. Корни из единицы §5.

Показательная и логарифмическая функции комплексной переменной Глава III ПРОСТЕЙШИЕ СВЕДЕНИЯ ОБ АЛГЕБРЕ ПОЛИНОМОВ §1. Полиномы от одной буквы §2.

Алгебраическое решение уравнений третьей и четвертой степени §3. Полиномы от нескольких букв Глава IV МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ §1. Матрицы и действия над ними §2.

Теория определителей §3. Линейная зависимость и линейная независимость строк (столбцов) §4.

Системы линейных уравнений общего вида §5. Дальнейшие свойства определителей §6.

Обращение квадратных матриц §7. Характеристический полином матрицы Глава V КВАДРАТИЧНЫЕ ФОРМЫ §1. Преобразование квадратичной формы к каноническому виду линейной подстановкой букв §2. Закон инерции квадратичных форм §3. Ортогональное преобразование квадратичной формы к каноническому §4.

Эрмитовы формы Глава VI ПОЛИНОМЫ И ДРОБИ §1. Теория делимости для полиномов от одной буквы §2. Производная §3.

Рациональные дроби §4. Интерполяция Глава VII СРАВНЕНИЯ В КОЛЬЦЕ ПОЛИНОМОВ И РАСШИРЕНИЯ ПОЛЕЙ §1. Сравнения в кольце полиномов над полем §2. Расширение полей Глава VIII ПОЛИНОМЫ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ. ПОЛИНОМЫ НАД ФАКТОРИАЛЬНЫМИ КОЛЬЦАМИ §1. Полиномы с целыми коэффициентами §2. Полиномы от одной буквы над факториальным кольцом Глава IX РАСПРЕДЕЛЕНИЕ КОРНЕЙ ПОЛИНОМА §1.

Существование корней в С §2. Распределение корней на плоскости комплексной переменной §3. Распределение вещественных корней полинома с вещественными коэффициентами §4. Обобщенная теорема Штурма §5. Приближенное вычисление корней полинома Глава X ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП §1.

Простейшие сведения §2. Нормальные подгруппы и факторгруппы §3. Гомоморфизм §4. Прямое произведение групп §5. Группы преобразований §6.

Свободная группа §7. Свободные произведения групп §8. Конечные абелевы группы §9. Конечно порожденные абелевы группы Глава XI СИММЕТРИЧЕСКИЕ ПОЛИНОМЫ §1. Выражение симметрических полиномов через основные §2. Значения симметрических полиномов от корней полинома §3.

Результант Глава XII ВЕКТОРНЫЕ ПРОСТРАНСТВА §1. Определения и простейшие свойства §2. Подпространства §3.

Линейные функции §4. Линейные отображения векторных пространств §5. Линейные операторы в векторном пространстве §6. Операторы в векторных пространствах над полем С комплексных чисел §7. Операторы в векторных пространствах над полем R вещественных чисел Глава XIII ЕВКЛИДОВО И УНИТАРНОЕ ПРОСТРАНСТВА §1.

Определения и простейшие свойства §2. Подпространства унитарного (или евклидова) пространства §3. Пространства, сопряженные с евклидовым и унитарным пространствами §4. Операторы в унитарном пространстве §5. Операторы в евклидовом пространстве §6. Преобразование уравнения гиперповерхности второго порядка к каноническому виду §7. Линейные отображения унитарного пространства в унитарное §8.

Объем параллелепипеда в евклидовом пространстве Глава XIV ЭЛЕМЕНТЫ АЛГЕБРЫ ТЕНЗОРОВ §1. Основные понятия §2. Действия над тензорами §3.

Симметричные и антисимметричные тензоры §4. Тензорные произведения векторных пространств Глава XV АЛГЕБРЫ §1. Общие сведения §2. Алгебра кватернионов §3. Внешняя алгебра Список литературы.

Уникальная ­­«Система обучения Физтеха» является одним из лучших подходов к образованию, что доказывает ее существование почти в неизменном виде уже более 60 лет. Получение фундаментального образования в области математики и физики, предварительное знакомство с избранной специализацией наряду с приобретением навыков самостоятельной работы уже на 4м курсе обеспечивают каждого студента объемом знаний и опыта полноценного ученого. Таким образом, к окончанию обучения студенты уже имеют значительные достижения в избранном ими направлении деятельности. 6 марта 2015 г.

Преподаватель: Официальный разбор билетов олимпиады «Физтех» 2015 года по физике. Запись прошедшего в онлайн-режиме разбора вариантов олимпиады «Физтех» 2015 года по физике для города Долгопрудный. Чивилёв Виктор Иванович - кандидат физико-математических наук, доцент кафедры общей физики МФТИ, член жюри Всероссийской олимпиады школьников по физике.

Гдз По Математике 8 Класс

Вы можете посмотреть другие лекции по ссылке - Группа ВК 'Абитуриенты МФТИ' - https://vk.com/abituru. 24 февраля 2015 г. Преподаватель: Подготовка к очному туру олимпиады «Физтех» 2015 года по физике. В лекции разобраны задачи олимпиады «Физтех» прошлых лет в рамках подготовки к олимпиады «Физтех» 2015 года по физике.

Чивилёв Виктор Иванович - кандидат физико-математических наук, доцент кафедры общей физики МФТИ, член жюри Всероссийской олимпиады школьников по физике. Вы можете посмотреть другие лекции по ссылке - Группа ВК 'Абитуриенты МФТИ' - https://vk.com/abituru. 21 февраля 2015 г. Преподаватель: Подготовка к очному туру олимпиады «Физтех» 2015 года по математике. В лекции разобраны задачи на делимость, комбинаторику и уравнения с параметром в рамках подготовки к олимпиаде 'Физтех' 2015 года.

Эта лекция откроывает цикл из 4-х лекций по подготовке к олимпиаде. Глухов Илья Викторович - преподаватель кафедры высшей математики МФТИ. Вы можете посмотреть другие лекции по ссылке - Группа ВК 'Абитуриенты МФТИ' - https://vk.com/abituru. 21 февраля 2015 г. Преподаватель: Официальный разбор онлайн-этапа олимпиады «Физтех» 2015 года по математике.

Запись прошедшего в онлайн-режиме разбора онлайн-этапа олимпиады «Физтех» 2015 года по математике. Вопросы можно будет задавать в режиме онлайн во время лекции. Бабичев Дмитрий Сергеевич - преподаватель кафедры математических основ управления МФТИ. Вы можете посмотреть другие лекции по ссылке - Группа ВК 'Абитуриенты МФТИ' - https://vk.com/abituru. 20 февраля 2015 г.

Преподаватель: Официальный разбор онлайн-этапа олимпиады «Физтех» 2015 года по физике. Запись прошедшего в онлайн-режиме разбора онлайн-этапа олимпиады «Физтех» по физике для 11 классов. Чивилёв Виктор Иванович - кандидат физико-математических наук, доцент кафедры общей физики МФТИ, член жюри Всероссийской олимпиады школьников по физике. Вы можете посмотреть другие лекции по ссылке - Группа ВК 'Абитуриенты МФТИ' - https://vk.com/abituru. 13 февраля 2015 г. Преподаватель: Подготовка к очному туру олимпиады «Физтех» 2015 года по математике. В лекции разобраны иррациональные и логарифмические уравнения и неравенства в рамках подготовки к олимпиаде 'Физтех' 2015 года.

Эта лекция откроывает цикл из 4-х лекций по подготовке к олимпиаде. Глухов Илья Викторович - преподаватель кафедры высшей математики МФТИ. Вы можете посмотреть другие лекции по ссылке - Группа ВК 'Абитуриенты МФТИ' - https://vk.com/abituru. 3 декабря 2014 г. Преподаватель: Подготовка к очному туру олимпиады «Физтех» 2015 года по математике. В лекции разобраны нелинейные системы уравнений и тригонометрические уравнения в рамках подготовки к олимпиаде 'Физтех' 2015 года. Эта лекция вторая из 4-х лекций по подготовке к олимпиаде.

Гдз По Математике 5 Класс

Глухов Илья Викторович - преподаватель кафедры высшей математики МФТИ. Вы можете посмотреть другие лекции по ссылке - Группа ВК 'Абитуриенты МФТИ' - https://vk.com/abituru.